| Python and Pygame |
|---|
| Pathfinding (12/7/2014) |
|
The problem of finding the best path between two points on a map which includes obstacles and
roads is an interesting one. A good source is Introduction to A* at
redblobgames.com. Another good introduction which I have
found particularly helpful is at flashgamedojo.com. My goal
here is to implement a path finding algorithm in python and to use pygame to provide visuals that allow
watching the algorithm as it works its way over the map.
The map I will be using is the following: |
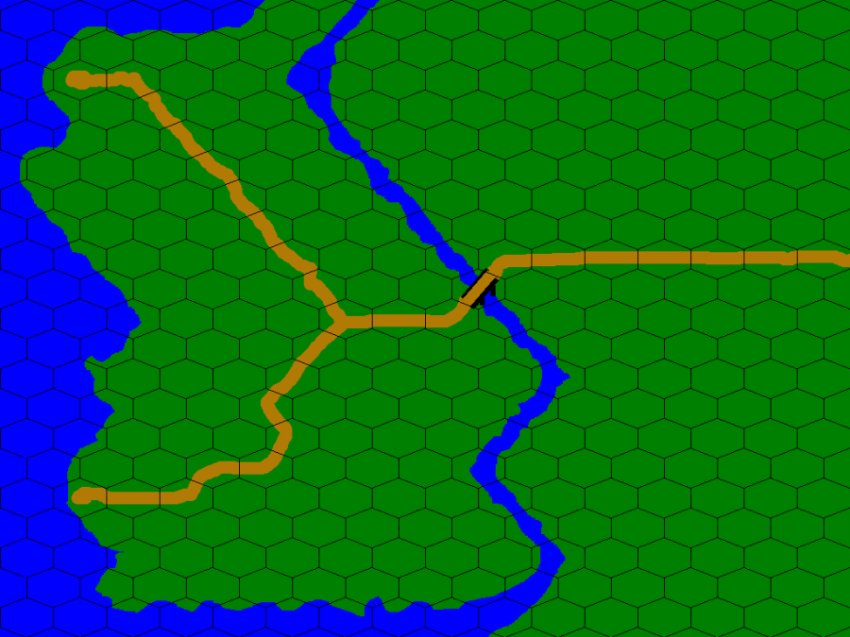
|
|
What you see on your screen is slightly smaller than the original which is 1024x768 pixels. As you can
see, a hexagonal grid has been overlaid on the map. The grid is 16 tiles wide and 21 tiles high. The pathfinding algorithm I am using is not very efficient, but it is very thorough and will always find a solution if one exists. I cannot claim to
have "invented" this algorithm; I worked out the details based on the descriptions of the various methods provided by
the sources I have read, somewhat inattentively, so neither can I claim that it represents a correct implementation of any recognized method. Let's just say it is something I hacked together.
The approach used is to calculate the weighted distance from the goal to every tile on the map. The weights assigned to a tile are based on the color pixel at the center of the hexagonal tile. The brown pixel inddicates a road, the green is grass, and blue is water. Water is treated as impassable in this example. We want the actors on the map to behave intelligently, so we want them to follow the road when it makes sense to do so. The road tiles are assigned a movement cost of 1 and the grass tiles are assigned a movement cost of 3. The algorithm proceeds as follows:
I. Creating a table of Movement CostThe first step is create an array 16x21 representing every tile on the map. The array will become a table of movement costs from the goal tile to every other walkable tile on the map. The array elements are initialized to a very large number. The initial value represent the largest allowable movement cost, so if you want to reduce the size of the region searched, you can initialize the array to a small number. For example, if the initial value is 9, that would limit the search to a range of three grass squares or 9 road squares. The goal tile is assigned a movement cost of zero and the evaluator is called for the goal tile.
II. The EvaluatorThe evaluator examines each neighboring tile in turn. If the neighboring tile is walkable, and if the movement cost of entering the neighboring tile does not exceed the current total cost to reach that tile from the goal tile, then the evaluator updates the movement cost table for the neighboring tile and recursively calls itself for the neighbor tile. It will require thousands of iterations to visit every tile, but eventually, the table will contain the movement cost from every tile to the goal tile. The actor simple has to move from its starting position to the goal tile by moving in the direction of decreasing total movement cost (like water flowing down a hill). Here is some python like pseudo code to illustrate the evaluator algorithm:
#
def evaluator(h,g):
# h = current tile (hex, tuple of row and column number in the map array)
# h = (row,column)
# g = target hex (goal)
global movement_cost_table
current_cost = movement_cost_table[h[0]h[1]]
max_cost = movement_cost_table[g[0]g[1]]
for i in range(6):
n = neighbor(h,i) # this function returns the address of neighboring tile i.
if tile_type(n) == GRASS:
current_cost += 3
elif tile_type(n) == ROAD:
current_cost += 1
if current_cost < max_cost :
if current_cost <= movement_cost_table[n[0]][n[1]]:
movement_cost_table[n[0][n[1]] = current_cost
evaluator(n,g):
III. Generate Path From TableOnce the movement_cost_table is finished, the path can be constructed from it:
def generate_path(h,g,mct):
# h = starting location
# g = goal
# mct = movement cost table
route = [h]
c = h
rng = mct[c[0]][c[1]]
while c != g:
for i in range(6):
n = neighbor(i)
if mct[n[0][n[1]] < mct[c[0]][c[1]] :
c = n
route += [c]
return route # list of tiles to follow
|

|
|
The example found a path that follows the road, crosses the bridge, then follows
the river bank to the target indicated by the square.
Using python and pygame, this run required about 2.4 seconds to find the path. There were over 10,000 recursive calls to the evaluator function. |
|
The complete demo program can be downloaded here.
The program was built using python2.7 and pygame1.9.1. Turning on the visualization of the pathfinding algorithm will cause the program to run very slowly. The longer the path, the longer it will take to find the desired solution. It can take as long as five minutes to find a path
across the board with visualization turned on. Without visualization, the longest paths only take about 3 seconds. Short paths are found with in couple of hundred milliseconds.
Here is a little video of the pathfinder in action. Click here.
|
Return to Games